Nel codice seguente è descritto come implementare una rotazione degli assi cartesiani o di vettori utilizzando tre angoli di Eulero.
I dettagli matematici di come sono definite le matrici di rotazione R non sono qui approfonditi, parleremo invece di come implementare praticamente queste trasformazioni in un codice python.
Una generica rotazione degli assi nello spazio può essere descritta da tre matrici R1, R2, R3 consecutive ognuna di un proprio angolo alpha, beta, gamma intorno ad un ass, la matrice che rappresenta la rotazione totale sarà il prodotto delle tre R=R3R2R1, la scelta degli assi di ciascuna singola operazione e la sequenza con cui le incateniamo determinano in modo univoco la trasformazione.
Riguardo all'espressione R=R3R2R1 si ricorda che il prodotto di matrici avviene da destra a sinistra, quindi R1 è la prima rotazione effettuata.
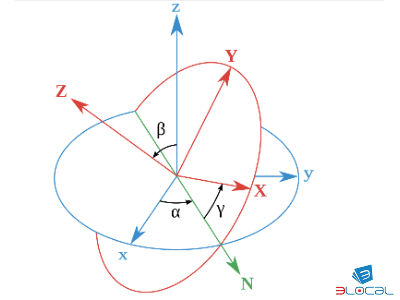
In seguito è utilizzata la convenzione ZXZ, cioé la rotazione dei tre assi viene effettuata prima intorno all'asse Z originario di un angolo alpha, la seconda di un angolo beta intorno al nuovo asse X, la terza di un angolo gamma inotrno al nuovo asse Z.
La matrice risultante R=R3R2R1 trasforma la base dei tre assi B nella base B'=RB dei nuovi assi, indichiamo di seguito le quantità primate come riferite al sistema riferimento ottenuto dalla rotazione.
La matrice inversa di R^-1 trasforma le coordinate di un vettore v espresse nella base B nelle coordinate dello stesso vettore nella nuova base B', v'=(vx',vy',vz')=R^-1(vx ,vy,vz) espresse nella base B'. Nel caso di una matrice la rotazione la matrice inversa è semplicemente la matrice trasposta (o la rotazione dell'angolo con segno inverso), R^-1=R^T, nel codice utilizziamo questa proprietà.
Nel codice definiamo una classe Rotazione3D che contiene tutti i parametri e i metodi che servono per effettuare i calcoli, definiamo quindi i tre attributi _alpha, _beta, _gamma che definiscono gli angoli e le tre rispettive matrici _Raplha, _Rbeta, _Rgamma.
La matrice totale _R3D è ottenuta attraverso il prodotto delle tre (utilizziamo qui la funzione di numpy.dot()) mentre la matrice per la rotazione dei vettori _R3Dinv è l'inversa di questa matrice (ottenuta qui tramite il prodotto delle matrici trasposte nell'ordine inverso).
Infine definiamo una funzione che, data una lista di vettori 3D, restituisca l'array dei vettori ruotati (nel codice "punti"), la funzione per ognuno dei vettori v effettua il prodotto numpy.dot(_R3Dinv, v).
Ultimo accesso a questo articolo il 19/07/2025
| Pierangelo Moraschi | p.moraschi@tiscali.it | Guarda il profilo social |



